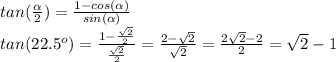Answer:
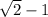
Explanation:
22.5 degrees is half of 45 degrees (special angle for which we know exactly the value of all three basic trigonometric functions (sine, cosine, and tangent).
So we start recalling the formula for tangent of a half angle:
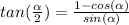
We need just the values of:
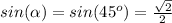
and of
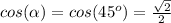
to answer the question. Then, we use those values in the original formula for tangent of a half angle: