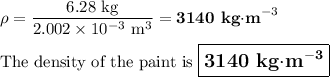Answer:
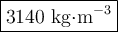
Step-by-step explanation:
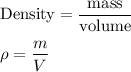
1. Mass of paint

2. Volume of paint
The paint is contained in a cylinder.
V = πr²h
(a) Radius of can
r = d/2 = (0.150 m)/2 = 0.0750 m
(b) Height of paint
h = 0.120 m - 0.007 m = 0.113 m
(c) Volume of paint
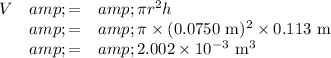
3. Density of paint