Question

Monique deposited her money in the bank to collect interest. The first month, she had $275 in her account. After the sixth month, she had $303.62 in her account. Use sequence notation to represent the geometric function.

an = 275 ⋅ (1.02)n−1
an = 275 ⋅ (0.10)n−1
an = 303.62 ⋅ (1.02)n−1
an = 303.62 ⋅ (1.10)n−1

Answer 1

`a_n = 275(1.02)^(n - 1)`

Explanation:

The geometric sequence is given explicitly by the formula:

`a_n = a(r)^(n - 1)`

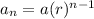
In the first month, Monique had $275 in her account.

`\implies \: a = 275`

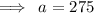
After the sixth month, she had $303.62 in her account.

`a_6 = 303.62`

`\implies \: a {r}^(5) = 303.62`

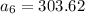
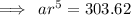
We solve for r,

`\frac{a {r}^(5) }{a} = (303.62)/(275)`

`\implies \: r = ( (303.62)/(275) )^{ (1)/(5) } = 1.02`

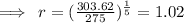
We fix everything back into the original formula to get:

`a_n = 275(1.02)^(n - 1)`