Question

Two parallel lines are cut by a transversal and form a pair of alternate exterior angles. One angle measures (6x + 5)° and the other measures (7x – 4)°. Explain how to determine what those angles actually measure?

Answer 1

Both angles measure 59°

Explanation:

All angles opposed by a vertice and alternate angles (exterior and exterior) and equal. That means that you can solve equaling both equations, since they measure the same. After finding X, substitute that value in the equations to find the angle measure

Answer 2

The alternate interior angles measure 59° each.

Explanation:

We know by given that those angles are alternate exterior angles, which means by definition those angles are equal.

That means both expressions form an equation

`6x+5=7x-4`

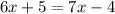
Let's solve for
`x`

`5+4=7x-6x\\x=9`

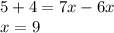
Now we have the value of the variable, we subsitute it in both angles expressions to find their degrees

`(6x+5)\°=(6(9)+5)\°=(54+5)\°=(59)\°\\(7x-4)\°=(7(9)-4)\°=(63-4)\°=(59)\°`

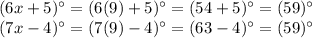
Therefore, the alternate interior angles measure 59° each.