Question

I need help ASAP

There are two fruit trees located at (3,0) and (−3, 0) in the backyard plan. Maurice wants to use these two fruit trees as the focal points for an elliptical flowerbed. Johanna wants to use these two fruit trees as the focal points for some hyperbolic flowerbeds. Create the location of two vertices on the y-axis. Show your work creating the equations for both the horizontal ellipse and the horizontal hyperbola. Include the graph of both equations and the focal points on the same coordinate plane.
Also you have to use vertices LESS THAN your focal point

Answer 1

See graph of the two conics in the attached picture

Explanation:

We create two vertices for the ellipse on the y-axis located at the points (0,2) and (0, -2) (marked with orange dots in the picture) and then create the equation for the ellipse such that its focus coincide with the place for the trees as requested. Recalling the formula for the position of the focus (c) for a horizontal ellipse of the form:
`(x^2)/(a^2) +(y^2)/(b^2) =1\\c=√(a^2-b^2) \\`

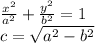
Since our
`b` value is 2 (choice of two vertices above), we have:

`c=√(a^2-b^2) \\3=√(a^2-2^2)\\3^2=a^2-4\\a^2=9+4=13`

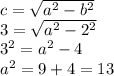
So now we can complete the equation of our ellipse with the trees at (-3,0) and (3,0):

`(x^2)/(13) +(y^2)/(4) =1`

Now we create the horizontal hyperbola of general form:
`(x^2)/(a^2) -(y^2)/(b^2) =1\\c=√(a^2+b^2)`

We request the same values for "c" and for "b" as we did with the ellipse:

`c=√(a^2+b^2) \\3=√(a^2+2^2)\\3^2=a^2+4\\a^2=9-4=5`

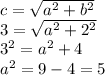
So now we can write the equation for this horizontal hyperbola:

`(x^2)/(5) -(y^2)/(4) =1`

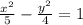
Both conics are plotted in the attached image, and their respective vertices that correspond to
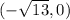`(-√(13) , 0)` and
`(√(13) , 0)` for the ellipse, and
`(-√(5) , 0)` and
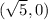`(√(5) , 0)` for the hyperbola, are indicated with blue dots and orange dots respectively.

The location of the trees (focus) is indicated with red dots.