Question

A ball is thrown vertically in the air with a velocity of 160ft/s. Use the projectile formula h=−16t2+v0t to determine at what time(s), in seconds, the ball is at a height of 384ft.

Answer 1

2 seconds

Explanation:

You are given an equation, a height, and a velocity. Using this you need to solve for t:

`384=-16t^2+160t\\16t^2-160t+384=0\\t^2-10t+24=0\\(t-6)(t-4)=0\\t=4, 6`

We get 2 answers for t. This is because the ball is at 384ft twice - once on its way up, and again on its way down. The ball is at (or above) 384ft for 6 - 4 = 2 seconds.

Answer 2

4 and 6 seconds

Explanation:

We have the following information about the problem:

initial velocity:
`v_(0)=160ft/s`

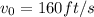
height:
`h=384ft`

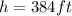
And the projectile formula is:

`h=-16t^2+v_(0)t`

substituting known values

`384=-16ft^2+160t`

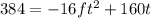
To simplify the equation we divide both sides by 16:

`(384)/(16) =(-16)/(16)t^2+(160)/(16)t`

`24=-t^2+10t`

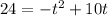
Now, we move all terms to the left:

`t^2-10t+24=0`

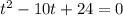
And we have a quadratic equation for the time that can be solved by factoring.

To factor we open two parenthesis and put
`t` o each, and we look for two numbers that multiplied result in
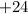`+24` and added together result in
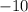`-10`. Those numbers are
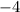`-4` and
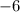`-6` (because (-4)(-6)=24 and -4+(-6)=-10)

So the factorization is as follows:

`(t-4)(t-6)=0`

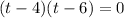
and by the zero product property (if two terms when multiplied result in zero, one of them or both are equal to zero):

`(t-4)=0`

⇒
`t=4`

`(t-6)=0`

⇒
`t=6`

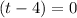
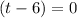
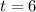
The times that the ball is at a height of 384 ft are 4 and 6 seconds.