Answer:
The answer to your question: Perimeter = 62.19 m
Explanation:
Data
DM = 10 √3
∠M = 75°
∠N = 45
Perimeter = ?
Process
The sum of the internal angles in a triangles equals 180°
∠D + ∠M + ∠N = 180
∠D = 75 + 45 = 180
∠D = 180 - 120
∠D = 60°
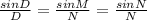
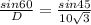
D =
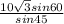
D = 21.21
![(sin D)/(D) = (sin 75)/(M) = \frac{sin 45}{10[tex]√(3)]() }[/tex]
}[/tex]
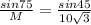
D =
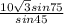
D = 23.66
Perimeter = 21.21 + 23.66 + 10

Perimeter = 62.19 m