Answer:
Distance between origin and point P(3, -4) is 5 units.
Solution:
We need to find distance between origin and point P (3, -4) .
We will be using distance formula. According to the distance formula , distance d between two points
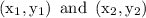 is given by
is given by
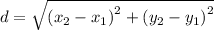
In given case two points are O ( 0 , 0 ) (origin) and P( 3 , -4) .
On applying distance formula
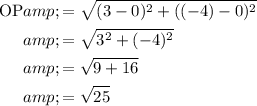
So OP = 5 units
Hence distance between origin and point P(3, -4) is 5 units.