Question

A family has two cars. During one particular week, the first car consumed 15 gallons of gas and the second consumed 35 gallons of gas. The two cars drove a

combined total of 1700 miles, and the sum of their fuel efficiencies was 60 miles per gallon. What were the fuel efficiencies of each of the cars that week?​

Answer 1

Fuel efficiencies of two cars in that week are 20 miles per gallon and 40 miles per gallon.

Solution:

Let the two cars of family be A and B.

Gas consumed by car A = 15 gallons

Gas consumed by car B = 35 gallons

Let’s assume number of miles car A drove in that week = x miles

Assume number of miles car B drove in that week = y miles

Given that two cars drove a combine of 1700 miles in that week.

So we can say,

x + y = 1700 --- eqn (1)

Fuel efficiency of any car =
`\frac{\text { Number of miles covered }}{\text { gallons of gas consumed }}`

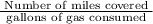
So fuel efficiency of car A =
`\frac{x \text { miles }}{15 \text { gallons }}`

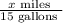
And fuel efficiency of car B =
`\frac{y \text { miles }}{35 \text { gallons }}`

Given that sum of efficiencies of two cars = 60 miles per gallons.

`(x)/(15)+(y)/(35)=60`

`(35 x+15 y)/(35 * 15)=60`

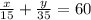
On cross-multiplication we get,

5(7x +3y) =
`15 * 35 * 60`

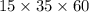
7x +3y = 6300 --------- eqn (2)

Now we have following two equations and two variable to be determine.

x + y = 1700 -------- (1)

7x +3y = 6300 -------- (2)

On modifying equation (1) we get

y = 1700 - x --------(3)

On substituting value of y from equation (3) in equation (2) we get

7x + 3(1700-x) = 6300

7x + 5100 – 3x = 6300

4x = 6300 – 5100

4x = 1200

x = 300

Substituting value of x in equation 3 to get value of y

y = 1700 – 300 = 1400

Fuel efficiency of car A =
`(x)/(15)` =
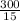`(300)/(15)` = 20 miles per gallon

Fuel efficiency of car B =
`(y)/(35)` =
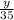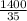`(1400)/(35)` = 40 miles per gallon.

Hence fuel efficiencies of two cars in that week are 20 miles per gallon and 40 miles per gallon.