Answer:
There cannot be unique price of an apple and an orange for which price of four apples and four oranges is $10 and price of 6 apples and 6 oranges is $ 12.
Solution:
Let’s first create linear equations from given information.
Let assume price of 1 apple = $x
And price of 1 orange = $y
For 4 apples and 4 oranges amount required is $10.
4x + 4y = 10
On simplification, we get
2x + 2y = 5 ------(1)
And for 6 apples and 6 oranges amount required is $12.
6x + 6y = 12
On simplification we get
x + y =2 ------(2)
So two required equations are
2x + 2y = 5 ------(1)
x + y =2 ------(2)
According to the system of linear equations ,
Two equations
 will have unique solution if
will have unique solution if
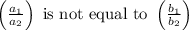
Let’s check our two equations for unique solution.
In our case
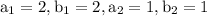
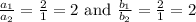
Since in our case
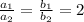
So our equation will not have unique solution.
Now let’s check
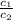
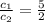
So final condition for our two linear equation is
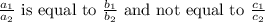
According to system if linear equation above condition is for no solution means equation (1) and equation (2) do not have any solution.
Hence there cannot be unique price of an apple and an orange for which price of four apples and four oranges is $10 and price of 6 apples and 6 oranges is $ 12.