Question

The length and breadth of a rectangle are in the ratio 3:2 respectively. If the sides of the rectangle are increased by 1 meter on each side, the ratio of the length to the breadth becomes 10:7. find the area of the original rectangle in square units.

Answer 1

The length and breadth of the rectangle are 18 m and 12 m.

SOLUTION:

Let the length and breadth of a rectangle be "l" and "b"

Given,length and breadth of the rectangle are in ratio 3 : 2

Then, length : breadth :: 3 : 2

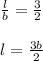`\begin{array}{l}{(l)/(b)=(3)/(2)} \\\\ {l=(3 b)/(2)}\end{array}` -- eqn 1

After changing the length and breadth by 1 meter on both sides, length and breadth becomes L+2 and b+2

Now, the ratio of length to breadth is 10 : 7

Length : breadth :: 10 : 7

`(l+2)/(b+2)=(10)/(7)`

`(l +2 ) * 7 = 10 * ( b + 2)`

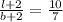
7l + 14 = 10b + 20

10b – 7l + 20 -14 = 0

10b – 7l + 6 =0 -- eqn (2)

Now, substitute “l” value in (2)

`10 b-7\left((3 b)/(2)\right)+6=0`

`10 b-(21 b)/(2)+6=0`

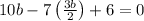
20b – 21b + 12 = 0

-b + 12 = 0

b = 12.

Substitute b value in (2)

10(12) – 7l + 6 = 0

120 + 6 = 7l

7l = 126

l = 18

hence, the length and breadth of the rectangle are 18 m and 12 m.