Question

If x=2/3 and x=-3 are the roots of the equation ax^2+7x+b=0 find the values of a and b

Answer 1

If x =
`(2)/(3)` and x = -3 are the roots of the equation, then values of a and b are 3, -6

SOLUTION:

Given, quadratic equation is
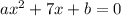`a x^(2)+7 x+b=0` and its roots are -3 ,
`(2)/(3)`

We know that, for any quadratic equation of form
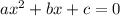`a x^(2)+b x+c=0` with roots
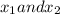`x_(1) and x_(2)` then,

Sum of roots
`(x_(1) +x_(2))` =
`(-b)/(a)`

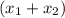Product of roots (
`x_(1) * x_(2))` =
`(c)/(a)`

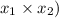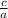
Now, for given quadratic equation
`x_(1)` = -3 and
`x_(2)` =
`(2)/(3)`

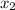hence Sum of roots =
`(-7)/(a)`

`x_(1) + x_(2) = (-7)/(a)`

`-3 + (2)/(3) = (-7)/(a)`

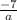
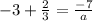
on solving we get "a" = 3

Now product of roots =
`x_(1) * x_(2) = (b)/(3)`

`-3 * (2)/(3) = (b)/(3)`

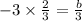
b = -6

hence, the values of a and b are 3, -6.