ANSWER:
Five times a number is added to two times it’s square. The value of “x” is either 8 or -10.5
SOLUTION:
Let the number be “x”
Given, Five times a number is added to two times it’s square.
Five times a number + two times it’s square .Hence we get
5x + 2x square
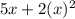
Also given that, result is 168. So the above equation is equal to 168

Let us find roots of above equation using quadratic formula.
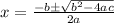
Here, a = 2, b = 5, c = -168
Substitute the values in formula we get
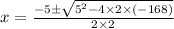
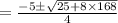
On simplification we get,

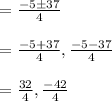
x = 8, -10.5
Hence, the value of x is either 8 or -10.5