ANSWER:
Twice a number is added to three times it’s square. The number is 2, -2.67
SOLUTION:
Let the number be x.
Given, twice a number is added to three times it’s square.
twice a number + three times it’s square
2
 number + 3
number + 3
 numbers square
numbers square
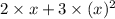
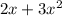
Also given that, result is 16. So the above equation is equal to 16
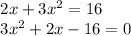
Let us find roots of above equation using quadratic formula.
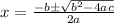
Here, a = 3, b = 2, c = -16
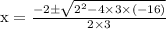
On simplification we get,
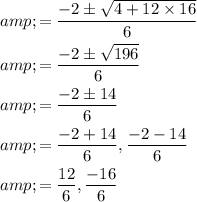
x = 2, -2.67
Hence, the value of "x" is either 2 or -2.67