Answer:
a. For equation
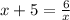 value of x are 1 and -6.
value of x are 1 and -6.
b. For equation
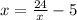 value of x are 3 and -8
value of x are 3 and -8
c. For equation
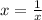 value of x are -1 and 1.
value of x are -1 and 1.
Solution:
a)Given equation is
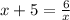
On cross multiplying we get,
x(x+5)=6
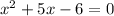
On splitting the middle term we get,
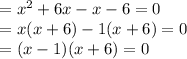
When x - 1 = 0 , x = 1
When x + 6 = 0 , x = -6
So two values of x which satisfies the given equation are 1 and -6.
b)Given equation is
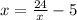
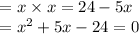
On splitting the middle term we get
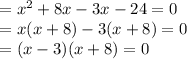
When x - 3 = 0 , x = 3
When x + 8 = 0 , x = -8
So two values of x which satisfies the given equation are 3 and -8.
c) Given equation is
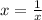
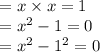
Using algebraic identity
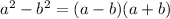 we get
we get
=(x-1)(x+1)=0
When x - 1 = 0 , x =1
When x + 1 = 0 , x = -1
So two values of x which satisfies the given equation are 1 and -1.