Question

When a number is added to its square the result is 90. Find the number.

Answer 1

♫ :::::::::::::::::::::::::::::: // Hello There ! // :::::::::::::::::::::::::::::: ♫

➷ We can form an equation:

x^2 + x = 90

Subtract 90 from both sides:

x^2 + x - 90 = 0

Now factorize:

(x + 10)(x - 9) = 0

Thus, x = 9 or x = -10

Either of these answers would work, but stick with 9 as your answer.

❄️

➶ Hope This Helps You!

➶ Good Luck (:

➶ Have A Great Day ^-^

↬ ʜᴀɴɴᴀʜ ♡

Answer 2

When a number is added to its square the result is 90. The number is 9, -10

SOLUTION:

Let the number be "x"

Given, a number is added to it’s square. This can be represented as,

number + it’s square

`x+x^(2)`

Also given that, result is 90. Hence the above equation is equal to 90

`\begin{array}{l}{x+x^(2)=90} \\ {x^(2)+x-90=0}\end{array}`

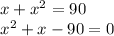
we can solve this equation by factorizing the equation.

`x^(2)+1 * x-9 * 10=0`

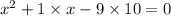
On rewriting the above equation, we get

`\begin{array}{l}{x^(2)+(10-9) * x-9 * 10=0} \\ {x^(2)+10 x-9 x-9 * 10=0}\end{array}`

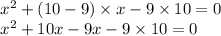
Taking “x” as common, we get

x(x + 10) -9(x + 10) = 0

(x + 10)(x – 9) = 0

x+10 = 0, x – 9 = 0

x = -10, 9

Hence, the values of x are 9, -10.