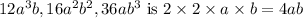Question

Find the greatest common factor of 12a^3b, 16a^2b^2, and 36ab^3

Answer 1

The greatest common factor of
`12 a^(3) b, 16 a^(2) b^(2), 36 a b^(3) \text { is } 4 a b`

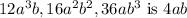
Solution:

To find the greatest common factor we have to find the prime factors of individual numbers and then find the number which is common to each given number.

Here the numbers are
`12 a^(3) b, 16 a^(2) b^(2), 36 a b^(3)`

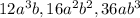
Let us find out the prime factors of each number .

`\begin{array}{l}{\text { Prime factors of } 12 a^(3) b=2 * 2 * 3 * a * a * a * b} \\ {\text { Prime factors of } 16 a^(2) b^(2)=2 * 2 * 2 * 2 * a * a * a * b * b} \\ {\text { Prime factors of } 36 a b^(3)=2 * 2 * 3 * 3 * a * b * b * b}\end{array}`

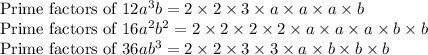
We can see that
`2 * 2 * \mathrm{a} * \mathrm{b}` is common to all the given numbers
`12 a^(3) b, 16 a^(2) b^(2), 36 a b^(3)`

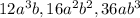
Therefore the greatest common factor of
`12 a^(3) b, 16 a^(2) b^(2), 36 a b^(3) \text { is } 2 * 2 * a * b=4 a b`