Question

A fish tank in a pet store has 22 fish in it. 7 are orange and 15 are white. Determine the probability that if we select 3 fish from the tank, at least 2 will be white.

Answer 1

We have a 55% of probably that 2 fish will be white.

Explanation:

That’s why we have 22 fish , 11 is the middle, so it is the 50%, 15 white fish are the 55% of 22 total fishes.

Answer 2

Approximately 77.2%.

Explanation:

At least two out of three fish are white means that

• Either two out of the three fish are white and the other one is orange, or
• All three fish are white.

How many ways to choose two out of fifteen objects (white fish in this case?)

The combination formula gives the number of unique ways to choose
`r` out of
`n` objects. Note that in case of combination (as opposed to permutation,) the order of the objects does not matter.

`\displaystyle {n \choose r} = (n!)/(r!(n-r)!) = (n (n - 1) \cdots (n - r +1))/(r(r-1) \cdots 1)`.

`\displaystyle \rm _(15)C_(2) = {15 \choose 2} = 105`.

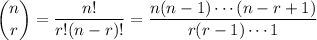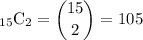How many ways to choose one out of seven objects (orange fish in this case?)

Similarly, by the combination formula

`\displaystyle \rm _(7)C_(1) = {7 \choose 1} = 7`.

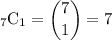How many ways to choose two out of fifteen white fish and one out of seven orange fish at the same time? Since both events happen at the same time, the result is the product of the two numbers of ways:

`105 * 7 = 735`.

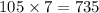Similarly, the number of ways of choosing three out of fifteen white fish will be:

`\displaystyle \rm _(15)C_(3) = {15 \choose 3} = 455`.

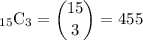It is not possible to choose both two and three white fish at the same time. In other words, one of the two situations may occur. Add the two numbers of ways to choose in each situation to find the total number of ways of choosing that satisfy the conditions.

`735 + 455 = 1190`.

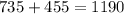How many possible ways to choose three objects out of twenty-two in total (including ones that do not satisfy the condition?)

`\displaystyle \rm _(22)C_(3) = {22\choose 3} = 1540`.

The probability of meeting the requirements will be equal to

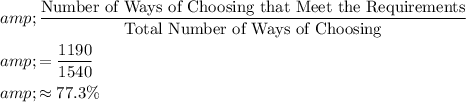`\begin{aligned} &\frac{\text{Number of Ways of Choosing} \text{ that Meet the Requirements}}{\text{Total Number of Ways of Choosing}}\\ &= (1190)/(1540) \\&\approx 77.3\%\end{aligned}`.