Question

Imagine a small child whose legs are half as long as her parent's legs. If her parent can walk at maximum speed V , at what maximum speed can the child walk?

a-v
b-v/2
c-2v
d-sqrt2* v
e-v/sqrt 2

Answer 1

The maximum speed can the child walk is v/sqrt 2

Step-by-step explanation:

Let the length of parent’s leg be L

Then the length of the child’s leg
`=(L)/(2)`

Maximum Speed at which the parent walks=V

To Find :

The maximum speed at which the child walks=?

Solution:

The Frequency of the simple pendulum

`f=(1)/(2 \pi)(\sqrt{(g)/(l)})`

`\text {Speed}=\frac{\text {distance}}{\text {time}}`

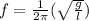
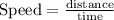
Speed of the parent

`V=L f_(p)`

`V=L\left((1)/(2 \pi)(\sqrt{(g)/(L)})\right)`

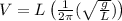
Speed of the child

`v=(L)/(2)\left((1)/(2 \pi)(\sqrt{(g)/(L / 2)})\right)`

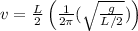
Now,

`(v)/(V)=\frac{(L)/(2)\left((1)/(2 \pi)(\sqrt{(g)/(L / 2)})\right)}{L\left((1)/(2 \pi)(\sqrt{(g)/(L)})\right)}`

`(v)/(V)=(√(2))/(2)`

`(v)/(V)=(√(2))/(√(2) √(2))`

`(v)/(V)=(1)/(√(2))`

`v=(V)/(√(2))`

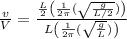
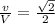
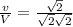
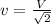
Result:

The maximum Speed at which the child can walk is
`(V)/(√(2))`