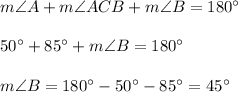Question

Answer the Blanks:

m∠A = 50m

∠ACB = 85

Answer Blank #1: Find ∠ADC

Answer Blank #2: Find ∠ CDB

Answer Blank #3: Find ∠ ACD

Answer Blank #4: Find ∠ BCD

Answer Blank #5: Find ∠ B


Use only numbers. Do not label your answers.

Answer 1

1. 90°

2. 90°

3. 40°

4. 45°

5. 45°

Explanation:

Given: ΔABC,

CD⊥AB,

m∠A=50°,

m∠ACB=85°

Solution:

1. ∠ADC is a right ange, because CD⊥AB, so

`m\angle ADC=90^(\circ)`

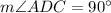
2. ∠CDB is a right ange, because CD⊥AB, so

`m\angle CDB=90^(\circ)`

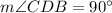
3. Consider triangle ACD. The sum of the measures of all interior angles is always 180°, so

`m\angle A+m\angle ADC+m\angle ACD=180^(\circ)\\ \\50^(\circ)+90^(\circ)+m\angle ACD=180^(\circ)\\ \\m\angle ACD=180^(\circ)-50^(\circ)-90^(\circ)=40^(\circ)`

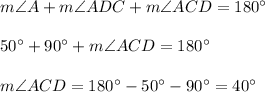
4. By Angle Addition Postulate,

`m\angle ACD+m\angle BCD=m\angle ACB\\ \\40^(\circ)+m\angle BCD=85^(\circ)\\ \\m\angle BCD=85^(\circ)-40^(\circ)=45^(\circ)`

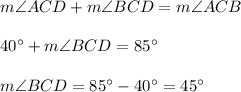
5. Consider triangle ABC. The sum of the measures of all interior angles is always 180°, so

`m\angle A+m\angle ACB+m\angle B=180^(\circ)\\ \\50^(\circ)+85^(\circ)+m\angle B=180^(\circ)\\ \\m\angle B=180^(\circ)-50^(\circ)-85^(\circ)=45^(\circ)`