Answer:
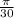 radians per minute.
radians per minute.
Step-by-step explanation:
In order to solve the problem you can use the fact that the angle in radians of a circumference is 2π rad.
The clock can be seen as a circumference divided in 12 equal pieces (because of the hour divisions). Each portion is
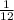
So, you have to calculate the angle between each consecutive hour (Let ∅ represent it). It can be calculated dividing the angle of the entire circumference by 12.
∅=
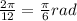
Now, you have to find how many pieces of the circumference are between 12 and 4 to calculate the angle (Because 4 o'clock is when the minute hand is in 12 and the hour hand is in 4)
There are 4 portions from 12 to 4, so the angle (Let α represent it) is:
α=
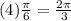
But the answer is asked in radians per minute. So you have to divide the angle by the amount of minutes between the hands of the clock at 4 o'clock.
There are 60 divisions in a clock for representing minutes, therefore in every portion there are:
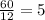 minutes
minutes
So, from the 12 mark to the 4 mark there are 20 minutes
The angle per minute is:
α=
 rad/min
rad/min
Notice that the minimum angle is the angle mesured clockwise.