Answer:
maximum at x=5
Explanation:
This path is parabolic (represented by a parabola since it is given by a quadratic expression).The parabola has the branches down since its leading coefficient is negative (-3), so the maximum value of this function will correspond to the vertex of the parabola.
We can use the definition for the vertex of a parabola to find it.
For a general parabola of the form:
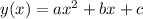 ,
,
the x-value of its vertex is given by the expression:
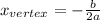
In our case, (since
 = -3, and
= -3, and
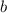 = 30) it becomes:
= 30) it becomes:
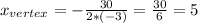
Therefore, the projectile will reach its maximum at x=5