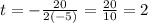Answer:
t = 2
Explanation:
Notice that this expression for the projectile's path is that of a quadratic function with negative leading term. The graph of it therefore consists of a parabola with the branches pointing down (due to he negative leading coefficient). Therefore, the maximum of such parabola will reside at its vertex.
Recall that the formula for the position of the vertex in a general parabolic function of the form:
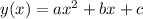 , is given by the expression:
, is given by the expression:
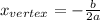
In our case, the variable "x" is in fact "t", the leading coefficient (
 ) is -5, and the coefficient for the linear term (
) is -5, and the coefficient for the linear term (
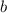 ) is 20.
) is 20.
Therefore, the maximum of the path will be when