Question

How does the graph of g(x) = (x − 2)3 + 7 compare to the parent function f(x) = x3?

Answer 1

First of all, a parent function refers to the simplest function of its type, for example, the parent function of any quadratic function is
`f(x)=x^(2)`.

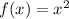So, in this case we have a cubic function, which parent function is
`f(x=x^(3)`.

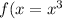Now, form the parent function we apply specific transformation to get other more complex functions, as the given

`g(x)=(x-2)^(3)+7`

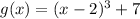
The transformations applied to the cubic parent function are just translations. The function was move 2 units to the right, and 7 units upwards.

Remember, if we subtract units from the x-variable, the function will move rightwards, if we sum unit to f(x), the function will move upwards.

So, basically these functions can be compared, because they belong to the same family of function, which are cubic, and basically we can get g(x) from f(x) by just applying certain transformations.

Answer 2

Translation 2 units to the right and 7 units up

Explanation:

Consider the parent function
`f(x)=x^3` and the function
`g(x)=(x-2)^3+7`

1. Translate the parent function f(x) two units to the right. The new function will be

`h(x)=(x-2)^3`

2. Translate the function h(x) 7 units up, then the translated function will have the expression

`g(x)=(x-2)^3+7`