Answer: Hello mate!
Clairaut’s Theorem says that if you have a function f(x,y) that have defined and continuous second partial derivates in (ai, bj) ∈ A
for all the elements in A, the, for all the elements on A you get:
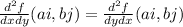
This says that is the same taking first a partial derivate with respect to x and then a partial derivate with respect to y, that taking first the partial derivate with respect to y and after that the one with respect to x.
Now our function is u(x,y) = tan (2x + 3y), and want to verify the theorem for this, so lets see the partial derivates of u. For the derivates you could use tables, for example, using that:
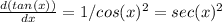
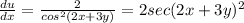
and now lets derivate this with respect to y.
using that
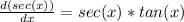
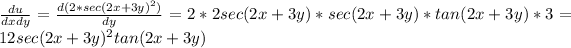
Now if we first derivate by y, we get:
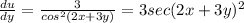
and now we derivate by x:
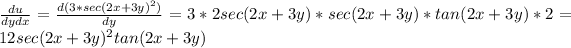
the mixed partial derivates are equal :)