The airplanes are 2726.68m apart.
Why?
To calculate how far are the planes apart, we need to find the angle between their displacements, then, we can use the law of cosines to solve the problem.

Now that we know the angle, we can use the law of cosines to find the distance between the two airplanes:
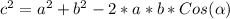
Also, we need to remember the formula to calculate distance:
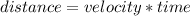
Substituting we have:

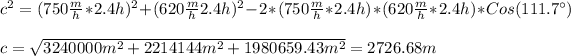
Hence, we have that the airplanes are 2726.68m apart.
Have a nice day!