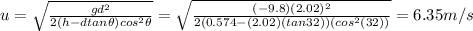Question

Salmon often jump waterfalls to reach their

breeding grounds.
Starting downstream, 2.02 m away from a
waterfall 0.574 m in height, at what minimum
speed must a salmon jumping at an angle of
32 ◦
leave the water to continue upstream?
The acceleration due to gravity is 9.81 m/s
2
.
Answer in units of m/s.

Answer 1

6.35 m/s

Step-by-step explanation:

The motion of the salmon is equivalent to that of a projectile, which consists of two independent motions:

- A horizontal motion with constant speed

- A vertical motion with constant acceleration (
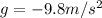`g=-9.8 m/s^2`, acceleration of gravity)

The horizontal velocity of the salmon is given by:

`v_x = u cos \theta`

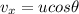
where

u = ? is the initial speed

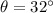`\theta=32^(\circ)` is the angle of projection

Then the horizontal distance covered by the salmon after a time t is given by

`d=v_x t =(u cos \theta) t`

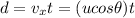
Or equivalently, the time taken to cover a distance d is

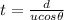`t=(d)/(u cos \theta)` (1)

Along the vertical direction, the equation of motion is

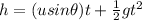`h = (u sin \theta) t + (1)/(2)gt^2` (2)

where

`u sin \theta` is the initial vertical velocity

If we substitute (1) into (2), we get:

`h = (u sin \theta) (d)/(cos \theta) + (1)/(2)g((d)/( ucos \theta))^2=d tan \theta + (gd^2)/(2u^2 cos^2 \theta)`

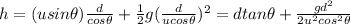
We now that in order to reach the breeding grounds, the salmon must travel a distance of

d = 2.02 m

reaching a height of

h = 0.574 m

Substituting these data into the equation and solving for u, we find the initial speed that the salmon must have:

`u =\sqrt{ (gd^2)/(2(h-d tan \theta) cos^2 \theta)}=\sqrt{((-9.8)(2.02)^2)/(2(0.574-(2.02)(tan 32))(cos^2(32)))}=6.35 m/s`