Answer:
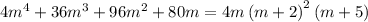 .
.
Explanation:
To factor the polynomial
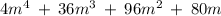 you must:
you must:
Factor out common term
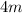 :
:
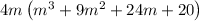
Next, factor
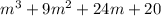 .
.
Since all coefficients are integers, apply the Rational Zeros Theorem.
The Rational Zero Theorem states that, if the polynomial
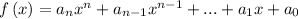 has integer coefficients, then every rational zero of
has integer coefficients, then every rational zero of
 has the form
has the form
 where
where
 is a factor of the constant term
is a factor of the constant term
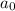 and
and
 is a factor of the leading coefficient
is a factor of the leading coefficient

Using the Rational Zero Theorem,
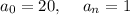
The dividers of
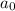 :
:
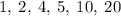
The dividers of
 : 1
: 1
Therefore, check the following rational numbers:
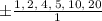
 is a root of the expression, so factor out
is a root of the expression, so factor out

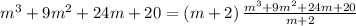
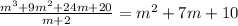
Next, factor
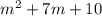

Therefore,
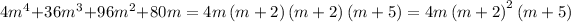 .
.