Answer:
See attached image
Explanation:
The question can be answered by plotting a large number of pairs (x, y) and connecting them with a trace, but most likely you are expected to analyse the local behavior and behaviour at the distance, in order to have the most relevant information about how the function behaves.
For the so called "local" behavior, you need to:
1) find the "zeroes" of the function (x-values for which the numerator of the function renders zero (0),
2) the "holes" in the function (x-values where the numerator and the denominator of the function are zero simultaneously.
3) the vertical asymptotes (for x-values where only the denominator becomes zero)
So, as you can se, it is fundamental to study the zeroes of both numerator and denominator:
Numerator is "x", therefore it will become zero when x = 0.
Denominator is x-9, therefore, it will become zero when x = 9
From the analysis above, our function posses a zero at x=0 (its graph then crosses the x-axis at x=0); and has a vertical asymptote at x=9.
We can study also what happens when the function approaches x=9 from the right and from the left, to see if the branches of the function close to that point go to +infinity or to -infinity.
Close to x=9 coming from the right, we can use the number 9.001 to evaluate what happens:
This large positive value tells us that the branch of the asymptote on the right side goes to +infinity *very positive y-values).
We can do something similar for the asymptotic branch on the left of x=9, by using the value 8.999 to evaluate (x):
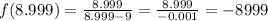which gives as a negative number indicating that the asymptotic branch on this side goes to -infinity (very negative y-values)
In order to find how the function behaves for values far away from the origin of coordinates, we need to study what happens with the quotient of the leading terms of numerator and denominator: leading term (and only term) of numerator is "x", and the leading term of the denominator is also "x", therefore, their quotient is :
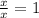which tells us that the function approaches the horizontal asymptote
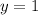as the function goes away from the origin.
With all this info, we can make a sketch of the function's graph as shown on the attached image, where the vertical asymptote is marked in red, the horizontal one in green, and the crossing of the x-axis as an orange dot