Question

If a ball is thrown into the air with a velocity of 34 ft/s, its height (in feet) after t seconds is given by y = 34t − 16t2. Find the velocity when t = 1.

Answer 1

If a ball is thrown into the air with a velocity of 34 feet per second, then velocity of the ball after 1 second is 2 feet per second

SOLUTION:

Given, a ball is thrown into the air with a velocity of 34 feet per second

Initial velocity (u) = 34 feet per second

And also given a relation between displacement and time =
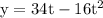`\mathrm{y}=34 \mathrm{t}-16 \mathrm{t}^(2)` --- eqn 1

We need to find the velocity when t = 1 ; v = ?

We know that, v = u + at and
`\mathrm{s}=\mathrm{ut}+(1)/(2) \mathrm{at}^(2)`

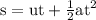
where v is instantaneous velocity and u is initial velocity

a is acceleration

t is time interval

s is displacement

using the displacement and time relation eqn (1) we get

Now, when t = 1, displacement s = 34(1) – 16(1)

`\mathrm{ut}+(1)/(2) \mathrm{at}^(2)=34-16`

`34 * 1+(1)/(2) * a * 1^(2)=18`

`34+(a)/(2)=18`

`\begin{array}{l}{(a)/(2)=18-34} \\\\ {(a)/(2)=-16} \\ {a=-16 * 2} \\ {a=-32}\end{array}`

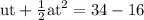
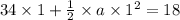
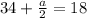
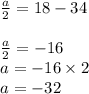
here, -ve sign indicates that object is in deceleration . so acceleration is -32 ft/s

now put a value in v = u + at

v = 34 + (-32)(1)

v = 34 – 32

v = 2 ft/s

Hence, velocity of the ball after 1 second is 2 ft/s