Question

QUICK EASY 25 POINTS!!

On a chapter test, Stephanie uses the rules of equation solving and inverse operations to solve the cubic equation below. The directions on the test are not very specific; however, they do say to give an exact solution. Stephanie is not sure if she should submit a decimal approximation or a simplified radical as the answer.

4x^3 = 756

1. What recommendation can you make to Stephanie regarding her answer to the cubic equation above? In your recommendation, explain what the term "exact" indicates with regards to the solution.

2. Solve the cubic equation from Stephanie’s test. Submit two solutions for the equation- a) your answer as a decimal approximation, rounded to the nearest hundredth, and b) as a simplified radical. Use substitution to check each version of your solution in the original equation.

3. After solving the test question and checking both the decimal solution and the simplified radical form, would you change your recommendation (in Part 1) to Stephanie regarding the format of her answer? Use complete sentences to explain your reasoning.

Answer 1

1. leave the radical symbol and don't try to convert it to a decimal form

2. The approximated value differs from the exact solution and doesn't give a true equation.

3. Depending on the case, if she needs a mathematical answer, the exact value should be used, but for more practical applications, the rounded decimal form would be more usable.

Explanation:

The step by step solution to the equation:

`4x^3=756\\x^3=(756)/(4) =189\\x=\sqrt[3]{189} \\x=\sqrt[3]{3^3*7} \\x=3*\sqrt[3]{7}`

1.- Exact solution means that if in the final step when solving for x the value of
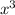`x^3` is not a perfect cube, one needs to leave it indicated as a radical expression (with the radical symbol).

in our case, the cubic root of 189 is not a perfect cube. The factor form of 189 is:
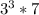`3^3*7`, so there is a perfect cube factor (
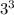`3^3`), but the other factor (7) is a prime number. Therefore 3 can get out of the root, while 7 stays inside.

2.- The equation was solved above, in exact form. Now to solve it giving a decimal approximation, we use a calculator to find the cubic root of 7, which is an irrational number with infinite number of decimals, the first of which we type here:
`\sqrt[3]{7} = 1.91293118...`

Therefore, the decimal approximation to the solving for x would be:

`x=3*\sqrt[3]{7}=3*1,91293118...=5.73879...=5.74`

Where we rounded to two decimals as requested.

When we replace the exact answer in the original expression, we get a perfect equality:

`4*x^3=756\\4* (3\sqrt[3]{7} )^3=756\\4*3^3*(\sqrt[3]{7} )^3=756\\4*27*7=756\\\\756=756`

While if we use the approximate answer, we get:

`4*x^3=756\\\\4*(5.74)^3=756\\\\4*189.119224=756\\756.476896=756`

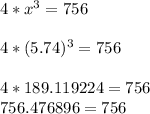
which is NOT a true equality.

3.- I would stick with the idea of showing the exact answer as answer to the mathematical equation. but for a practical case (for example she needs to by some material as a result of her equation solving, it would be more practical to take the numerical approximation to the store, instead of a cubic root of a number.