Question

The lifetime of a 2-volt non-rechargeable battery in constant use has a Normal distribution with a mean of 516 hours and a standard deviation of 20 hours. Ninety percent of all batteries have a lifetime less than 541.60 hours.

Answer 1

True

Explanation:

Data

mean (
`\mu`) = 516 hours

standard deviation (
`\sigma`) = 20 hours

expected lifetime (X) = 541.6 hours

In the figure attached, standard normal distribution table can be seen. Z is computed as follows:

`Z = (X - \mu)/(\sigma)`

`Z = (541.6 - 516)/(20)`

`Z = 1.28`

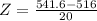
In table can be seen that the area between 0 and 1.28 is 0.3997, or simply 0.4. The area until Z = 0 is 0.5; so, the total area until Z = 1.28 is 0.9. That means 90% of batteries would have 541.6 lifetime hours.