Question

A rocket is launched upward so that its distance, in feet, above the ground after t seconds is represented by the function below. What is its maximum height? h(t)=−16t2+320t

Answer 1

1600 ft

Explanation:

We are given that a rocket is a launched upward so that its distance(feet) above the ground after t seconds is represented by the function

`h(t)=-16t^2+320t`

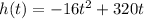
We have to find the maximum height.

Substitute h(t)=0

`-16t(t-20)=0`

`t=0,t-20=0\implies t=20`

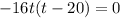
When t=0 it means the rocket is at ground launch.

When t= 20 s.

Total time taken by rocket=20 s.

Half of the time taken to reach maximum height and half of the time taken to reach ground back.

Therefore, time taken by rocket to reach maximum height=
`(20)/(2)=10s`

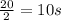
Substitute t=10 in given function

Then we get

h(10)=-16(10)^2+320(10)=-1600+3200=1600 ft[/tex]

Hence, the maximum height=1600 ft

Answer 2

Answer: 1600 feet.

Explanation:

Given : A rocket is launched upward so that its distance, in feet, above the ground after t seconds is represented by the function
`h(t)=-16t^2+320t`

To find : its maximum height.

First we differentiate the given function , we get

`h'(t)=(2)(-16)t+320=-32t+320`

Put
`h'(t)=0`, we get

`-32t+320=0\\\\\Rightarrow\ t=(-320)/(-32)=10`

Hence, at t=10 , rocket achieves its maximum height.

`\text{Maximum Height =}h(t)=-16\left(10\right)^(2)+320\left(10\right)\\\\=-1600+3200=1600`

Hence, its maximum height = 1600 feet.