1 Answer

Lilgodwin · Answer 1 · 2020-12-25T23:35:21+0000

Answer:

(5√(x))/(x^4)

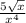
Explanation:

The given expression is

(5)/(√(x^7))

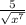
We need to find the simplified form of the given expression.

Using product property of exponent we get,

$(5)/(√(x^6\cdot x))$
$[\because a^ma^n=a^(m+n)]$

$(5)/(√(x^6)\cdot √(x))$ (Distributive property)

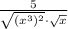
$(5)/(√((x^3)^2)\cdot √(x))$
$[\because (a^m)^n=a^(mn)]$

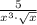
$(5)/(x^3\cdot √(x))$

Multiply numerator and denominator by
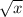√(x) to rationalize denominators.

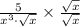
$(5)/(x^3\cdot √(x))* (√(x))/(√(x))$

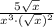
$(5√(x))/(x^3\cdot (√(x))^2)$

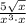
$(5√(x))/(x^3\cdot x)$

(5√(x))/(x^4)

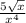
Therefore, the simplified form of given expression is
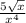(5√(x))/(x^4) .

Please log in or register to add a comment.