Answer:
The values are a=1 b=10 c=25 and solving the expression we get x=-5
Step-by-step explanation:
Given equation;
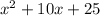
Solution:
The above equation can be written as
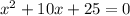
This equation is in the form of
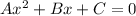
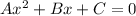 is the general quadratic equation.
is the general quadratic equation.
Comparing the above equation we get
A=1, B=10 and C=25
To find value of “x” we use the formula as
=
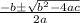
Substitute the values of a, b and c in the above equation we get
=
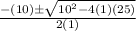
=
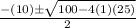
=
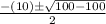
=
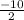
=-5
Results:
Thus the values are A=1, B=10, C=25 and X=-5