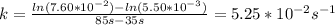Answer:
5.25*10^-2 s^-1
Step-by-step explanation:
For a first order reaction the rate of reaction just depends on the concentration of one specie [B] and it’s expressed as :
![-(d[B])/(dt)=k[B] - - - -(d[B])/([B])=k*dt](https://img.qammunity.org/2020/formulas/chemistry/high-school/54qm6jery2x1v12be8ln2c85u9iu1wsdrz.png)
if we integrate between the initial concentration and the concentration at any time we get:
![\int\limits^B_B \,-( d[B] )/([B])= \int\limits^t_t \, k*dt](https://img.qammunity.org/2020/formulas/chemistry/high-school/7go5uox8ed5t7q1zi3sd8gy69lbowarb0w.png)
Solution:
![-(ln[B]-ln[B]_(o))=kt](https://img.qammunity.org/2020/formulas/chemistry/high-school/vzmxuvyb8h692s4hwoum33snlljom9c2ix.png) (equation 1)
(equation 1)
You can clear this equation to get a equation for [B] at any time but because we want to estimate k is easier to use this expression.
In equation 1 we don’t know the value of [B]o so we can’t clear directly to get the value of K, but we know the concentration at two different times. With this information, we can get a system with two mathematical unknowns and two equations that we can solve.
Equations:
(1)
![-(ln[B]_(1)-ln[B]_(o))=k*t_(1)](https://img.qammunity.org/2020/formulas/chemistry/high-school/yx2h9vpqxcim3amaior2u2ndjef8w2rm2w.png)
(2)
![-(ln[B]_(2)-ln[B]_(o))=k*t_(2)](https://img.qammunity.org/2020/formulas/chemistry/high-school/y7cn2qpy5s5yk7fitthf55ytxuf67tlw8t.png)
With
![[B]_(1)= 7.60 *10^(-2) M, t_(1)=35s](https://img.qammunity.org/2020/formulas/chemistry/high-school/zvk3w86qzyq0js8vg3kg6hjxdmq60riycb.png)
![[B]_(2)= 5.50*10^(-3) M, t_(2)=85s](https://img.qammunity.org/2020/formulas/chemistry/high-school/jtanl6fxjdm3xdwrefrb0j0xr8e8qw404i.png)
From (1)
![ln[B]_(o)=k*t_(1)+ln[B]_(1)](https://img.qammunity.org/2020/formulas/chemistry/high-school/t53x7kqe6p86jwyimmrwlhzi6rxlfq96tt.png)
Replacing this value for
![ln[B]_(o)](https://img.qammunity.org/2020/formulas/chemistry/high-school/q42mj3dxdskggowyeexvjmes9o56w5r7lz.png) on (2) we get
on (2) we get
![-ln[B]_(2)+( k*t_(1)+ln[B]_(1))=k*t_(2)](https://img.qammunity.org/2020/formulas/chemistry/high-school/rwi6cqwlryzcz94ptpxzthxkeoucg4349d.png)
Organizing
![-ln[B]_(2)+ ln[B]_(1)= k*t_(2)- k*t_(1)](https://img.qammunity.org/2020/formulas/chemistry/high-school/lavyfhbjkdkpfntp4zuthbzxs6ypc38z76.png)
With k equals to
![k=(ln[B]_(1)- ln[B]_(2))/(t_(2)-t_(1))](https://img.qammunity.org/2020/formulas/chemistry/high-school/gap72x32kynainb1nohp86bakh9tjvzah9.png)