Answer
angle made by the horizontal = 30°
velocity = 5 m/s
distance = 7 m
Vertical component (V y) = 5 sin (30°) = 2.5 m/s
Horizontal component(V x) = 5 cos (30° ) = 4.33 m/s
Applying
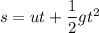
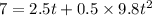
t = 0.967 s
b) Distance from base
=
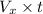
=
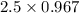
= 2.42 m
c) You can find final vertical velocity
V= u + gt
V = 9.8 × 0.967
v = 9.48 m/s
Final velocity =
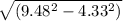
v = 8.433 m/s
Final angle
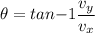
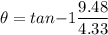
θ = 65.41°