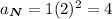Answer:
The curvature is
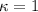
The tangential component of acceleration is
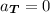
The normal component of acceleration is
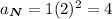
Explanation:
To find the curvature of the path we are going to use this formula:
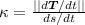
where
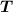 is the unit tangent vector.
is the unit tangent vector.
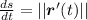 is the speed of the object
is the speed of the object
We need to find
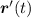 , we know that
, we know that
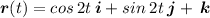 so
so
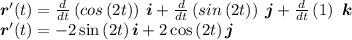
Next , we find the magnitude of derivative of the position vector
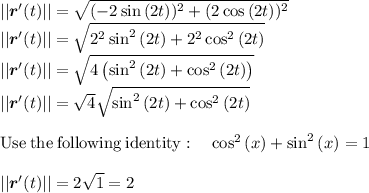
The unit tangent vector is defined by
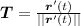
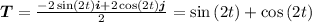
We need to find the derivative of unit tangent vector
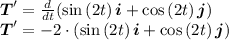
And the magnitude of the derivative of unit tangent vector is
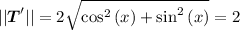
The curvature is
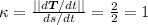
The tangential component of acceleration is given by the formula
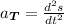
We know that
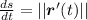 and
and
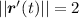
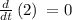 so
so
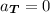
The normal component of acceleration is given by the formula
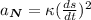
We know that
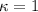 and
and
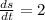 so
so