Question

In a shipment of 56 vials, only 13 do not have hairline cracks. If you randomly select 3 vials from the shipment, in how many ways can at least one of the 3 selected vials have a hairline crack if the order of selection does not matter?

Answer 1

Answer: 27434

Explanation:

Given : Total number of vials = 56

Number of vials that do not have hairline cracks = 13

Then, Number of vials that have hairline cracks =56-13=43

Since , order of selection is not mattering here , so we combinations to find the number of ways.

The number of combinations of m thing r things at a time is given by :-

`^nC_r=(n!)/(r!(n-r)!)`

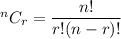
Now, the number of ways to select at least one out of 3 vials have a hairline crack will be :-

`^(13)C_2\cdot ^(43)C_(1)+^(13)C_(1)\cdot ^(43)C_(2)+^(13)C_0\cdot ^(43)C_(3)\\\\=(13!)/(2!(13-2)!)\cdot(43!)/(1!(42)!)+(13!)/(1!(12)!)\cdot(43!)/(2!(41)!)+(13!)/(0!(13)!)\cdot(43!)/(3!(40)!)\\\\=(13*12*11!)/(2*11!)\cdot (43)+(13)\cdot(43*42*41!)/(2*41!)+(1)(43*42*41*40!)/(6*40!)\\\\=3354+11739+12341=27434`

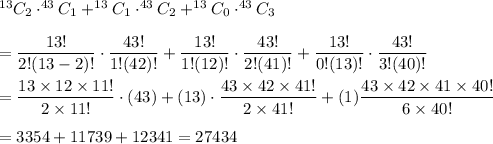
Hence, the required number of ways =27434