Question

A professor has learned that nine students in her class of 27 will cheat on the exam. She decides to focus her attention on ten randomly chosen students during the exam.

What is the probability that she finds at least one of the students cheating? (Round your intermediate calculations and final answers to 4 decimal places.)

Answer 1

The probability is 0.9827

Explanation:

The probability of the variable X that says the number of students cheating follow a Binomial distribution, because there are:

• 10 randomly chosen students or n identical and independent events
• A probability of 9/27 that the student is going to cheat or a probability of 1/3 of success

So, the probability P(x) that x students are going to cheat is calculated as:

`P(x)=(n!)/(x!(n-x)!)*p^(x)*(1-p)^(n-x)`

`P(x)=(10!)/(x!(10-x)!)*(1/3)^(x)*(1-(1/3))^(10-x)`

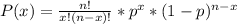
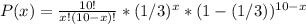
Then, the probability P that she finds at least one of the students cheating is calculated as:

P = P(x≥1) = P(1) + P(2) + P(3) + P(4) + P(5) + P(6) + P(7) + P(8) + P(9)

That also can be calculated as:

P = P(x≥1) = 1 - P(x<1) = 1 - P(0)

Therefore, P(0) is calculated as:

`P(0)=(10!)/(0!(10-0)!)*(1/3)^(0)*(1-(1/3))^(10-0)`

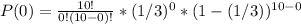
P(0) = 0.0173

Finally, P is equal to:

P = 1 - 0.0173 = 0.9827