Question

The path of a baseball, hit 3 feet above ground, is modeled by the function f(x)=−0.01x2+x+3, where f(x) represents the vertical height of the ball and x is the horizontal distance. How far across the field, in feet, will the ball travel before hitting the ground? Round to two decimal places.

Answer 1

102.92 feet

Explanation:

x is the horizontal distance [what we want to find]

f(x) represents the vertical height

Since, we want the horizontal distance traveled [x] before hitting ground [vertical height is 0, so f(x) = 0]

We want:

`f(x)=-0.01x^2+x+3`

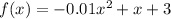
We will use quadratic formula to solve this. Quadratic Formula is:

`x=(-b+-√(b^2 -4ac) )/(2a)`

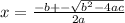
Where a is coefficient of x^2 and b is coefficient of x and c is the constant

Now, let's solve:

`x=(-b+-√(b^2 -4ac) )/(2a)\\x=(-1+-√((1)^2 -4(-0.01)(3)) )/(2(-0.01))\\x=102.92,-2.92`

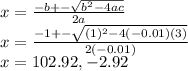
We disregard the negative solution [no neg distance] and take 102.92 feet as our answer