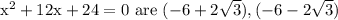Question

Identify the x-intercepts of the function below f(x)=x^2+12x+24

Answer 1

x-intercepts of
`\mathrm{x}^(2)+12 \mathrm{x}+24=0 \text { are }(-6+2 √(3)),(-6-2 √(3))`

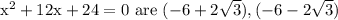
SOLUTION:

Given,
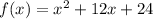`f(x)=x^(2)+12 x+24` -- eqn 1

x-intercepts of the function are the points where function touches the x-axis, which means they are zeroes of the function.

Now, let us find the zeroes using quadratic formula for f(x) = 0.

`X=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

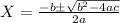
Here, for (1) a = 1, b= 12 and c = 24

`X=\frac{-(12) \pm \sqrt{(12)^(2)-4 * 1 * 24}}{2 * 1}`

`\begin{array}{l}{X=(-12 \pm √(144-96))/(2)} \\\\ {X=(-12 \pm √(48))/(2)} \\\\ {X=(-12 \pm √(16 * 3))/(2)} \\\\ {X=(-12 \pm 4 √(3))/(2)} \\ {X=(2(-6+2 √(3)))/(2), (2(-6-2 √(3)))/(2)} \\\\ {X=(-6+2 √(3)),(-6-2 √(3))}\end{array}`

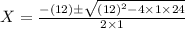
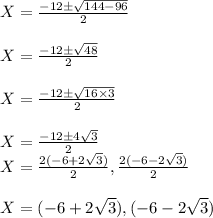
Hence the x-intercepts of
`\mathrm{x}^(2)+12 \mathrm{x}+24=0 \text { are }(-6+2 √(3)),(-6-2 √(3))`