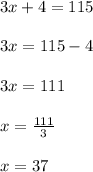Question

Two parallel lines are crossed by a transversal. Horizontal and parallel lines y and z are cut by transversal x. At the intersection of lines y and x, the bottom right angle is 115 degrees. At the intersection of lines z and x, the uppercase left angle is (3 x + 4) degrees. What is the value of x? x = 21 x = 28 x = 35 x = 37

Answer 1

Fourth Option x=37

Explanation:

edge 2021

Answer 2

Answer: Last option.

Explanation:

See the figure attached.

Given two parallel lines, you need to remember that, by definition, when two parallel lines are cut by a transversal, the interior angles formed on opposite side of the transversal are called "Alternate interior angles".

Alternate interior angles are congruent.

You can observe in the figure attached that the angle
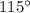`115\°` and the angle
`(3 x + 4)\°` are Alternate interior angles. Then, you can say that:

`3 x + 4=115`

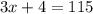
Finally, you must solve for "x". Then:

`3 x + 4=115\\\\3x=115-4\\\\3x=111\\\\x=(111)/(3)\\\\x=37`