Question

The height of 5th grade boys is normally distributed with mean μ=57 inches and standard deviation σ=2 inches. What is the probability that the height of a randomly selected 5th grade boy will be between 53 inches and 61 inches?

Answer 1

0.9544

Explanation:

Mean = μ=57

Standard deviation σ=2

Formula :
`z=(x-\mu)/(\sigma)`

At x = 53

`z=(53-57)/(2)`

`z=-2`

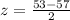
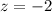
Refer the z table

P(z<-2)=0.0228

At x = 61

`z=(61-57)/(2)`

`z=2`

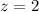
Refer the z table

P(z<2)=0.9772

We are suppose to find the probability that the height of a randomly selected 5th grade boy will be between 53 inches and 61 inches.

P(53<x<61)=P(-2<z<2)=P(z<2)-P(z<-2) = 0.9772 - 0.0228=0.9544

Hence the probability that the height of a randomly selected 5th grade boy will be between 53 inches and 61 inches is 0.9544