Answer:
1071202 miles
Explanation:
Circumference of planet A =
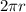
We are given that Planet A has a circumference of 93,480 miles.
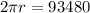
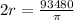
Since we know that twice the radius is diameter
So,
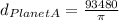
Now we are given that Its moon has a diameter that is approximated to be 1/ 8 that of Planet A.
So,
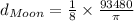
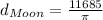
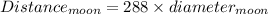
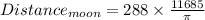
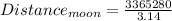
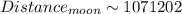
Hence the approximate distance of the moon from Planet A is 1071202 miles