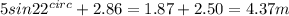Answer:
(a) Height is 4.47 m
(b) Height is 4.37 m
Solution:
As per the question:
Initial velocity of teh ball,
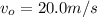
Angle made by the ramp,

Distance traveled by the ball on the ramp, d = 5.00 m
Now,
(a) At any point on the projectile before attaining maximum height, the velocity can be given by the eqn-3 of motion:
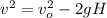
where
H =
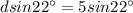
g =

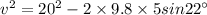
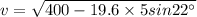 = 19.06 m/s
= 19.06 m/s
Now, maximum height attained is given by:
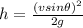
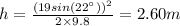
Height from the ground =
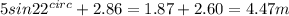
(b) now, considering the coefficient of friction bhetween ramp and the ball,
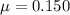 :
:
velocity can be given by the eqn-3 of motion:

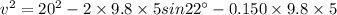
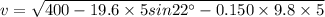 = 18.7 m/s
= 18.7 m/s
Now, maximum height attained is given by:
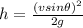

Height from the ground =