Answer:
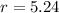 --- Radius
--- Radius
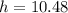 --- Height
--- Height
Step-by-step explanation:
Given
Object: Can (Cylinder)
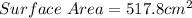
Required
Maximize the volume
The surface area is:
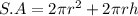
Substitute 517.8 for S.A
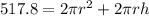
Divide through by 2
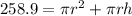
Factorize:
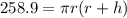
Divide through by


Make h the subject
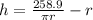 --- (1)
--- (1)
Volume (V) is calculated as:
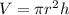
Substitute (1) for h
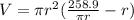
Open Bracket
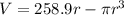
Differentiate V
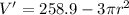
Set V' to 0
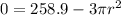
Collect Like Terms
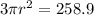
Divide through by 3
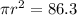
Divide through by

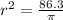
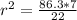
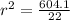
Take square root of both sides
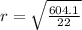
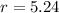
Recall that:
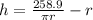
Substitute 5.24 for r
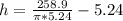
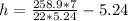
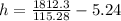
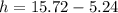
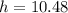
Hence, the dimension that maximize the volume is:
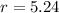 --- Radius
--- Radius
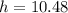 --- Height
--- Height