Question

Find the point equidistant from the three points (-6,0),(-3,1) and (0,0).​

Answer 1

The point equidistant from the three points (-6,0),(-3,1) and (0,0) is (-3,-3)

Solution:

The given three points are A (-6, 0), B (–3, 1) and C (0, 0)

Let P (x, y) be the point equidistant from these three points.

Distance between two points is given as

`\mathrm{D}=\sqrt{\left(\mathrm{x}_(2)-\mathrm{x}_(1)\right)^(2)+\left(\mathrm{y}_(2-) \mathrm{y}_(1)\right)^(2)}`

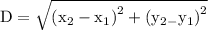
Where
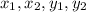`x_(1), x_(2), y_(1), y_(2)` are the x and y co-ordinates

The distance between A (-6, 0) and P(x, y) is:

Using the distance formulae,

`\mathrm{D}=\sqrt{(\mathrm{x}+6)^(2)+(\mathrm{y}-0)^(2)}`

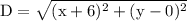
On taking square root we get,

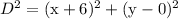`D^(2)=(\mathrm{x}+6)^(2)+(\mathrm{y}-0)^(2)` --- eqn 1

The distance between B(-3, 1) and P(x, y) is:

`\mathrm{D}=\sqrt{(\mathrm{x}+3)^(2)+(\mathrm{y}-1)^(2)}`

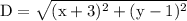
On taking square root we get

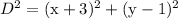`D^(2)=(\mathrm{x}+3)^(2)+(\mathrm{y}-1)^(2)` --- eqn 2

The distance between C(x, y) and P (0, 0) is:

`\mathrm{D}=\sqrt{(\mathrm{x}-0)^(2)+(\mathrm{y}-0)^(2)}`

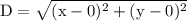
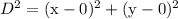`D^(2)=(\mathrm{x}-0)^(2)+(\mathrm{y}-0)^(2)` -- eqn 3

By equating equation 1 = equation 2 to find the value of y

`(x+6)^(2)+(y-0)^(2)=(x-0)^(2)+(y-0)^(2)`

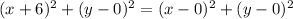
In both the expression
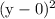`(\mathrm{y}-0)^(2)` is common so we can cancel it.

`(\mathrm{x}+6)^(2)=(\mathrm{x}-0)^(2)`

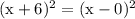
On expanding we get,

`x^(2)+36+12 \mathrm{x}=x^(2)`

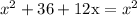
12x = -36

x = -3.

Now find the value of y using equation 3.

`\begin{array}{l}{x^(2)+y^(2)=0} \\ {(-3)^(2)+y^(2)=0} \\ {3^(2)=-y^(2)} \\ {y=-3}\end{array}`

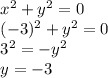
Hence the required points are (-3,-3).