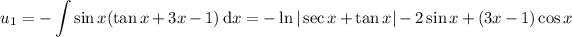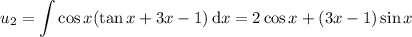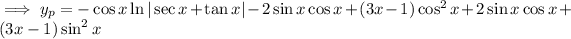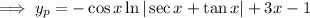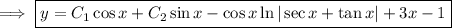Question

Using variation of parameters method to find particular solution d^2y/dx^2+y=tanx+3x-1

Answer 1

The corresponding homogeneous equation

`(\mathrm d^2y)/(\mathrm dx^2)+y=0`

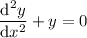
has characteristic equation

`r^2+1=0`

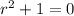
which admits two roots,
`r=\pm i`, so the characteristic solution is

`y_c=C_1\cos x+C_2\sin x`

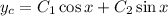
So we know two fundamental solutions,
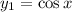`y_1=\cos x` and
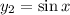`y_2=\sin x`. These two solutions have Wronskian determinant

`W(y_1,y_2)=\begin{vmatrix}\cos x&\sin x\\-\sin x&\cos x\end{vmatrix}=\cos^2x+\sin^2x=1`

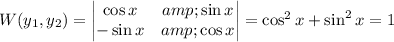
so they are linearly independent.

We use variation of parameters to find a particular solution
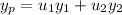`y_p=u_1y_1+u_2y_2`, where

`u_1=-\displaystyle\int\sin x(\tan x+3x-1)\,\mathrm dx=-\ln|\sec x+\tan x|-2\sin x+(3x-1)\cos x`

`u_2=\displaystyle\int\cos x(\tan x+3x-1)\,\mathrm dx=2\cos x+(3x-1)\sin x`

`\implies y_p=-\cos x\ln|\sec x+\tan x|-2\sin x\cos x+(3x-1)\cos^2x+2\sin x\cos x+(3x-1)\sin^2x`

`\implies y_p=-\cos x\ln|\sec x+\tan x|+3x-1`

`\implies\boxed+3x-1`