Answer:
1)
1st Error: In going from Step 3 to Step 3.
Reason: Negative sign is not distributed inside the brackets.
2nd Error: In going from Step 5 to Step 6
Reason: Sign of the number is not changed while moving to other side of inequality,
2)
a) 12=-4(-6x-3) and x+5=-5x+5
b) -(7-4x)=9 and 5x+34=-2(1-7x) and -8=-(x+4)
Explanation:
Question 1)
The given inequality is:
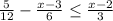
Step 1: Making the denominators common for all fractions
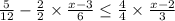
This step is done correctly in the given solution.
Step 2: Simplifying
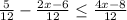
This step is done correctly in the given solution
Step 3: Multiplying both sides by 12, and simplifying.
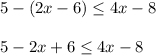
First error is made in this step. While opening the brackets, the negative sign should be distributed inside the bracket, which will change the signs.
Step 4: Simplification:

Step 5: Moving Common terms to one side and simplifying
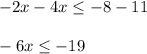
Error was made in this step. When a number is moved to other side, its sign will be changed.
Step 6: Dividing both sides by -6
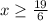
Conclusion:
1st Error: In going from Step 3 to Step 3.
Reason: Negative sign is not distributed inside the brackets.
2nd Error: In going from Step 5 to Step 6
Reason: Sign of the number is not changed while moving to other side of inequality,
Question 2:
In the Equation 2: 12=-4(-6x-3), when -4 will be multiplied inside the brackets, the 12 on eft hand side will cancel the 12 that will appear on right hand side, giving a result that will lead to x = 0.
Same is the case with Equation 6: x+5=-5x+5, 5 on both sides will cancel out leaving x = 0.
So, 2nd and 6th equations will have the same solution.
In Equation 1, on expanding the bracket and moving 7 to other side, we get a relation: 4x = 16
In Equation 3, on simplifying the right hand side, and carrying common terms to one side, we get the relation: - 9x = -36
In Equation 5, on expanding the bracket and simplifying the relation is reduced to 4 = x
It can be observed that all these 3 equations have the same solution i.e. x = 4
So, the following set of Equations have the same solution:
a) 12=-4(-6x-3) and x+5=-5x+5
b) -(7-4x)=9 and 5x+34=-2(1-7x) and -8=-(x+4)